Hello friends👋 In this article we'll be going through the key part in building a calculator app; which is infix to postfix conversion.
Say that we are to build a basic calculator app as shown in figure below; that accepts the following operators: subtraction, addition, multiplication, division and brackets.
An example expression that a user can therefore input is:
9 – 3 * 5 + 2 * (6/2).
A question then arises; how do we write the logic for the calculation to be performed in such a way that the precedence of the operators is observed; having in mind that the computer will be performing these instructions sequentially.
Converting the expression from infix to postfix will allow us to observe the right order of operations during evaluation; hence the precedence and associativity rules will be observed.
Infix vs Postfix
An infix expression is one whereby the operator comes in between the two operands its working on. This is the usual (common) way in which we write expressions.
Whereas a postfix expression is one whereby the operator comes after the two operands its working on.
Example:
A + B
3 + 2 : the + operator is coming in between the two operands (3 and 2); infix expression.
A ,B , +
3, 2, + : the + operator comes after the two operands (3 and 2), ; postfix expression.
In the above examples, the operands are only two, given more than two operands, then the infix to postfix conversion will follow the steps below:
Step 1
We will create a list to store the postfix expression and a stack to store the operators.
Step 2
Scan the expression from Left to Right.
As we scan:
2.1: Check if the value is a double(or integer). If its a double(or integer) directly add it onto the postfix list.
2.2: If the value is an operator; then:
2.1.1: If the stack is empty; directly push it onto the stack.
2.1.2: Else if the stack is NOT empty. Check the operator precedence. Comparing the precedence of the operator at the top of the stack, with the incoming operator.
Operator Precedence (BODMAS).
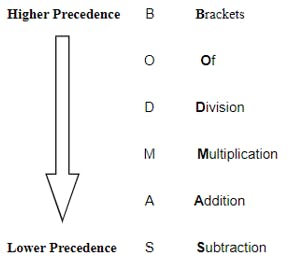
If the operator is of higher precedence than the operator at the top of the stack, directly push it onto the stack;
Whereas if the operator is of lower precedence than the the operator at the top of the stack. First pop the stack; adding the popped value onto the postfix list. Then compare again the precedence of the operator and the operator at the top of the stack. Iterate till the operator is of higher precedence compared to the value at the top of the stack. Then, push it onto the stack. i.e. on the stack, we can only have a lower precedence operator, followed by a higher precedence operator.
2.1.3: If its an opening bracket ( push it directly onto the stack, and if it’s the closing bracket ); pop from the stack while adding the operators onto the post fix list till the closing bracket is reached.
Having in mind the logic above; given the infix expression below:
3 + 2 * 3
The post fix expression will therefore be evaluated as follows:
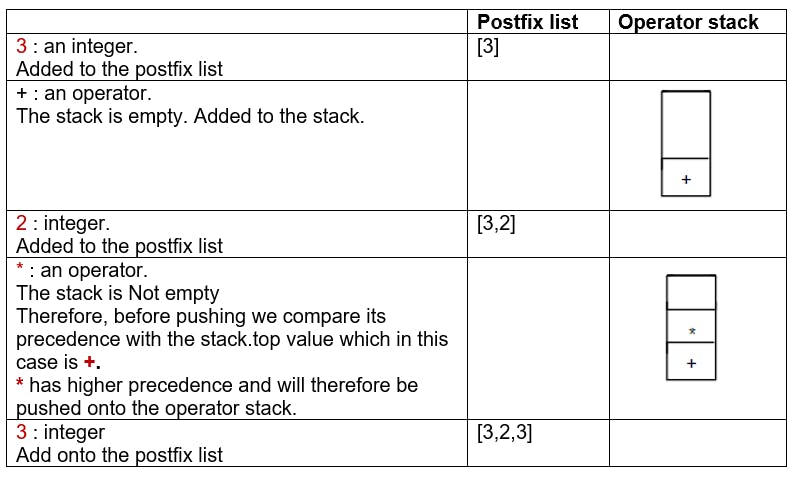
At this point, we are at the end of the Left to Right scan, and the stack still has some operators.
We therefore pop values from the stack as we append them to the postfix list till the stack is empty:
After the first pop, the postfix list is: [3,2,3,*]
The stack still has one value, we pop again: [3,2,3,*,+]
The stack is now empty and the final postfix expression is therefore:[3,2,3,*,+]
I have my postfix expression, what next?
Once the postfix expression is obtained. Then, the actual calculation of the expression can be done.
Step 1
Create a stack to store the doubles(integers).
Step 2
Given the postfix expression, scan it from Left to Right.
Step 3
As we scan, if it’s a number, then push it into the stack, if it an operator, pop the top two expressions from the stack, evaluate them with the operator and push the result back onto the stack.
Continuing with our example above:
Scanning the post fix expression [3,2,3,*,+] :
Starting from Left:
3, an integer; pushed into the stack
2, an integer; pushed into the stack
3, an integer; pushed into the stack
* , an operator. Pop the stack to get the top two numbers which are 3 and 2. Evaluate 2 * 3 then push the result 6 back onto the stack.
+, an operator, pop the top two values, 6 and 3; Evaluate 6 + 3 then push the result 9 back onto the stack.
The scan is complete there is only one value in the stack, 9. This will be the final result.
Another example:
3 + 4 (4 * 2 + 6)
At this point you might be wondering is there an alternative to using the stack in the infix to postfix conversion. Sure, there is but that would require multiple scans of the expressions before arriving at the final answer. Using the stack, we scan the expression from Left to Right only once to arrive at the postfix expression and thus the use of stack proves to be more efficient.
Any thoughts and comments, would love to hear those!
Happy coding 🤠
Credits: Cover photo by Black Ice.